聚类

聚类和分类的区别:

分类其实是从特定的数据中挖掘模式，作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器，一开始的时候可能什么都不过滤，在日常使用过程中，我人工对于每一封邮件点选“垃圾”或“不是垃圾”，过一段时间，Gmail就体现出一定的智能，能够自动过滤掉一些垃圾邮件了。这是因为在点选的过程中，其实是给每一条邮件打了一个“标签”，这个标签只有两个值，要么是“垃圾”，要么“不是垃圾”，Gmail就会不断研究哪些特点的邮件是垃圾，哪些特点的不是垃圾，形成一些判别的模式，这样当一封信的邮件到来，就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。 聚类的的目的也是把数据分类，但是事先我是不知道如何去分的，完全是算法自己来判断各条数据之间的相似性，相似的就放在一起。在聚类的结论出来之前，我完全不知道每一类有什么特点，一定要根据聚类的结果通过人的经验来分析，看看聚成的这一类大概有什么特点。

聚类问题

所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。

K-means聚类算法

聚类算法属于非监督学习的一种，聚类算法有很多种，大概有几十种聚类算法。 K-means是聚类算法中的最常用的一种，它运算速度快，但是只能应用于连续的数据。 K-means的算法的计算过程如下： 1，需要一个k值 来指定我们首先希望簇的个数（或者说首先定多少个中心点） 2，从数据集中随机选择k个数据点作为质心 3，计算每个点离质心的距离，选择最近的质心成一簇 4，每个簇算出新的质心 5，如果新的质心与老质心的距离小于某个阈值，则认为聚类达到期望 6，重复3-5步骤

"距离"的概念

K-means中的距离，是个相似度或者相异度的概念，根据数据集的特征（比如标量、向量、枚举分类等）决定如何计算距离。 常用的距离有： 1，欧几里德距离： 对于数值型、标量的数据，就应该用欧氏距离。 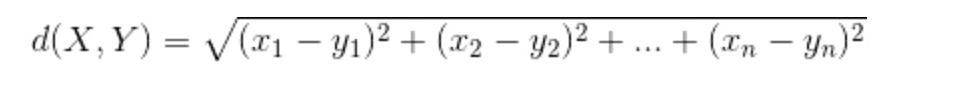选择欧几里德距离计算距离,如果数据集的单位不一致，就会有问题。 所以要进行数据的标准化将数据按比例缩放，使之落入一个小的特定区间。去除数据的单位限制，将其转化纯数值型数据 标准化方法最常用的有两种： min-max标准化（离差标准化）：对原始数据进行线性变换，是结果落到【0，1】区间，转换方法为 X'=（X-min）/（max-min），其中max为样本数据最大值，min为样本数据最小值。 z-score标准化（标准差标准化）：处理后的数据符合标准正态分布（均值为0，方差为1），转换公式：X减去均值，再除以标准差 2，余弦相似度（向量夹角）： 对于向量型的数据，使用标量型的距离公式就不合适了，一种流行的方法是计算两个向量的向量夹角。 我们高中学过 两个向量的余弦是两个向量的点乘除以两个向量模长的乘积。 （两个向量的点乘也可以用向量矩阵X的转秩乘向量矩阵Y来表示） 这里要注意，余弦度量度量的不是两者的相异度，而是相似度，所以我们应该使用他的反函数，即acos。 3，Jaccard： 就是交集除以并集 |S ∩ T|/|S ∪ T| 还有一些其他的距离计算方式：切比雪夫距离、曼哈顿距离、马哈拉诺比斯距离、调整后的余弦相似度等等

demo

from collections import defaultdict
from random import uniform
# from math import acos
from numpy import *



def point_avg(points):
    """
    Accepts a list of points, each with the same number of dimensions.
    NB. points can have more dimensions than 2

    Returns a new point which is the center of all the points.
    """
    dimensions = len(points[0])

    new_center = []

    for dimension in xrange(dimensions):
        dim_sum = 0  # dimension sum
        for p in points:
            dim_sum += p[dimension]

        # average of each dimension
        new_center.append(dim_sum / float(len(points)))

    return new_center


def update_centers(data_set, assignments):
    """
    Accepts a dataset and a list of assignments; the indexes
    of both lists correspond to each other.
    Compute the center for each of the assigned groups.
    Return `k` centers where `k` is the number of unique assignments.
    """
    new_means = defaultdict(list)
    centers = []
    for assignment, point in zip(assignments, data_set):
        new_means[assignment].append(point)

    for points in new_means.itervalues():
        centers.append(point_avg(points))

    return centers


def assign_points(data_points, centers):
    """
    Given a data set and a list of points betweeen other points,
    assign each point to an index that corresponds to the index
    of the center point on it's proximity to that point.
    Return a an array of indexes of centers that correspond to
    an index in the data set; that is, if there are N points
    in `data_set` the list we return will have N elements. Also
    If there are Y points in `centers` there will be Y unique
    possible values within the returned list.
    """
    assignments = []
    for point in data_points:
        shortest = 10  # positive infinity
        shortest_index = 0
        for i in xrange(len(centers)):
            val = distance(point, centers[i])
            if val < shortest:
                shortest = val
                shortest_index = i
        assignments.append(shortest_index)
    return assignments


def distance(a, b):
    """
    """
    # d
    dimensions = len(a)
    _sum = 0
    for dimension in xrange(dimensions):
        difference_sq = (a[dimension] - b[dimension]) ** 2
        _sum += difference_sq
    return sqrt(_sum)

    # acos
    # difference_sq = dot(a,b)/(linalg.norm(a)*linalg.norm(b))
    # return  acos(difference_sq)



def generate_k(data_set, k):
    """
    Given `data_set`, which is an array of arrays,
    find the minimum and maximum for each coordinate, a range.
    Generate `k` random points between the ranges.
    Return an array of the random points within the ranges.
    """
    centers = []
    dimensions = len(data_set[0])
    min_max = defaultdict(int)

    for point in data_set:
        for i in xrange(dimensions):
            val = point[i]
            min_key = 'min_%d' % i
            max_key = 'max_%d' % i
            if min_key not in min_max or val < min_max[min_key]:
                min_max[min_key] = val
            if max_key not in min_max or val > min_max[max_key]:
                min_max[max_key] = val

    for _k in xrange(k):
        rand_point = []
        for i in xrange(dimensions):
            min_val = min_max['min_%d' % i]
            max_val = min_max['max_%d' % i]

            rand_point.append(uniform(min_val, max_val))

        centers.append(rand_point)

    return centers


def k_means(dataset, k):
    k_points = generate_k(dataset, k)
    assignments = assign_points(dataset, k_points)
    old_assignments = None
    while assignments != old_assignments:
        new_centers = update_centers(dataset, assignments)
        old_assignments = assignments
        assignments = assign_points(dataset, new_centers)
    return assignments