from numpy import exp, array, random, dot
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
random.seed(1)
synaptic_weights = 2 * random.random((3, 1)) - 1
for iteration in xrange(10000):
output = 1 / (1 + exp(-(dot(training_set_inputs, synaptic_weights))))
synaptic_weights += dot(training_set_inputs.T, (training_set_outputs - output) * output * (1 - output))
print 1 / (1 + exp(-(dot(array([1, 0, 0]), synaptic_weights))))
本文我会解释这个神经网络是怎样炼成的，所以你也可以搭建你自己的神经网络。也会提供一个加长版、但是也更漂亮的源代码。 不过首先，什么是神经网络？人脑总共有超过千亿个神经元细胞，通过神经突触相互连接。如果一个神经元被足够强的输入所激活，那么它也会激活其他神经元，这个过程就叫“思考”。 我们可以在计算机上创建神经网络，来对这个过程进行建模，且并不需要模拟分子级的生物复杂性，只要观其大略即可。为了简化起见，我们只模拟一个神经元，含有三个输入和一个输出。 
我们将训练这个神经元来解决下面这个问题，前四个样本叫作“训练集”，你能求解出模式吗？?处应该是0还是1呢？ 
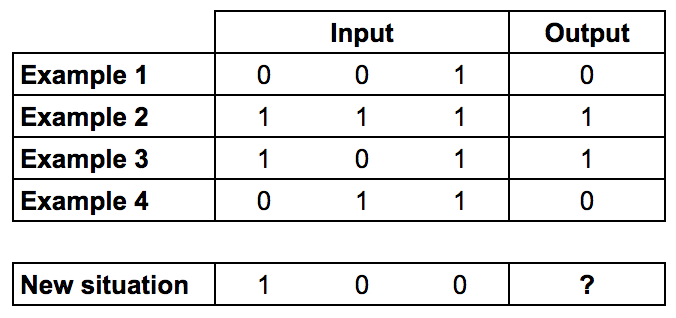或许已经发现了，输出总是与第一列的输入相等，所以?应该是1。 训练过程 问题虽然很简单，但是如何教会神经元来正确的回答这个问题呢？我们要给每个输入赋予一个权重，权重可能为正也可能为负。权重的绝对值，代表了输入对输出的决定权。在开始之前，我们先把权重设为随机数，再开始训练过程： 从训练集样本读取输入，根据权重进行调整，再代入某个特殊的方程计算神经元的输出。 计算误差，也就是神经元的实际输出和训练样本的期望输出之差。 根据误差的方向，微调权重。 重复10000次。 
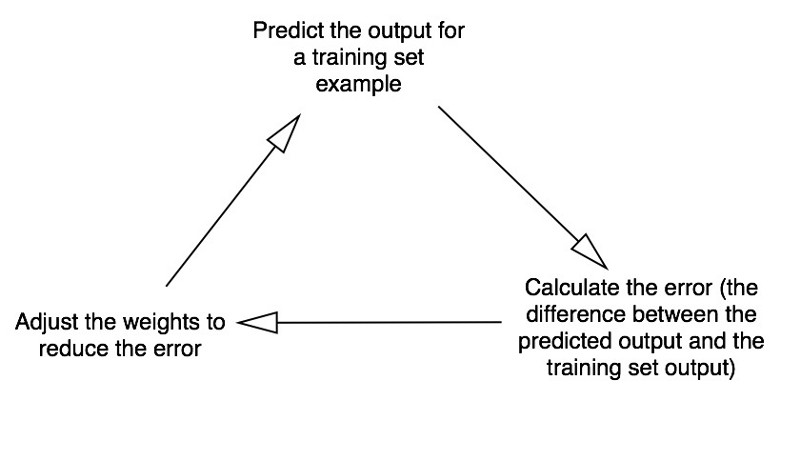最终神经元的权重会达到训练集的最优值。如果我们让神经元去思考一个新的形势，遵循相同过程，应该会得到一个不错的预测。 计算神经元输出的方程 你可能会好奇，计算神经元输出的人“特殊方程”是什么？首先我们取神经元输入的加权总和： 
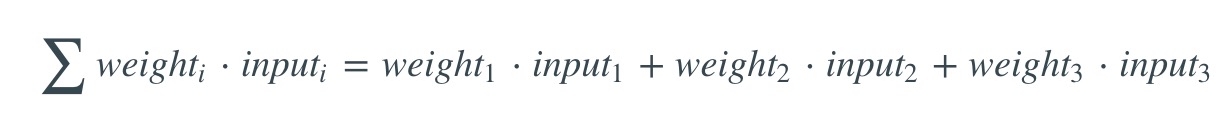接下来我们进行正规化，将结果限制在0和1之间。这里用到一个很方便的函数，叫Sigmoid函数： 
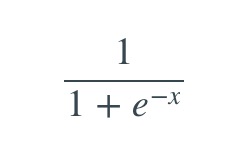igmoid函数是S形的曲线： 
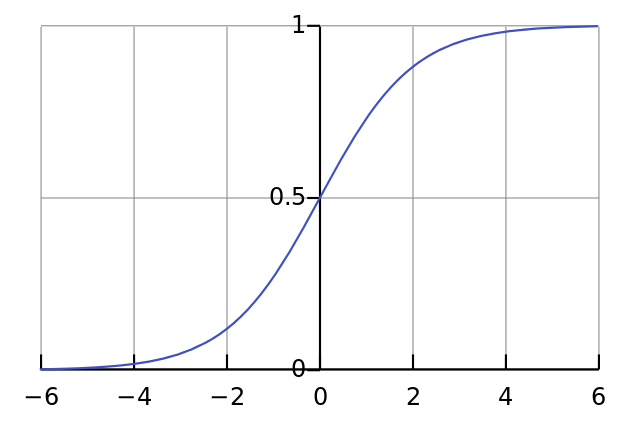将第一个公式代入第二个，即得最终的神经元输出方程： 
调整权重的方程 在训练进程中，我们需要调整权重，但是具体如何调整呢？就要用到“误差加权导数”方程： Adjustweightsby=error⋅input⋅SigmoidCurveGradient(output) Adjustweightsby=error⋅input⋅SigmoidCurveGradient(output) 为什么是这个方程？首先我们希望调整量与误差量成正比，然后再乘以输入(0-1)。如果输入为0，那么权重就不会被调整。最后乘以Sigmoid曲线的梯度，为便于理解，请考虑： 我们使用Sigmoid曲线计算神经元输出。 如果输出绝对值很大，这就表示该神经元是很确定的（有正反两种可能）。 Sigmoid曲线在绝对值较大处的梯度较小。 如果神经元确信当前权重值是正确的，那么就不需要太大调整。乘以Sigmoid曲线的梯度可以实现。 Sigmoid曲线的梯度可由导数获得： SigmoidCurveGradient(output)=output⋅(1−output) SigmoidCurveGradient(output)=output⋅(1−output) 代入公式可得最终的权重调整方程： Adjustweightsby=error⋅input⋅output⋅(1−output) Adjustweightsby=error⋅input⋅output⋅(1−output) 实际上也有其他让神经元学习更快的方程，这里主要是取其相对简单的优势。 构建Python代码 尽管我们不直接用神经网络库，但还是要从Python数学库Numpy中导入4种方法： exp： 自然对常数 array： 创建矩阵 dot：矩阵乘法 random： 随机数 比如我们用array()方法代表训练集：
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
.T函数就是矩阵转置。我想现在可以来看看美化版的源代码了，最后我还会提出自己的终极思考。源代码中已经添加了注释逐行解释。注意每次迭代我们都一并处理了整个训练集，以下为完整的Python示例：
from numpy import exp, array, random, dot
class NeuralNetwork():
def __init__(self):
# 随机数发生器种子，以保证每次获得相同结果
random.seed(1)
# 对单个神经元建模，含有3个输入连接和一个输出连接
# 对一个3 x 1的矩阵赋予随机权重值。范围-1～1，平均值为0
self.synaptic_weights = 2 * random.random((3, 1)) - 1
# Sigmoid函数，S形曲线
# 用这个函数对输入的加权总和做正规化，使其范围在0～1
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
# Sigmoid函数的导数
# Sigmoid曲线的梯度
# 表示我们对当前权重的置信程度
def __sigmoid_derivative(self, x):
return x * (1 - x)
# 通过试错过程训练神经网络
# 每次都调整突触权重
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
for iteration in xrange(number_of_training_iterations):
# 将训练集导入神经网络
output = self.think(training_set_inputs)
# 计算误差（实际值与期望值之差） error = training_set_outputs - output
# 将误差、输入和S曲线梯度相乘
# 对于置信程度低的权重，调整程度也大
# 为0的输入值不会影响权重
adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))
# 调整权重
self.synaptic_weights += adjustment
# 神经网络一思考
def think(self, inputs):
# 把输入传递给神经网络
return self.__sigmoid(dot(inputs, self.synaptic_weights))
if __name__ == "__main__":
# 初始化神经网络
neural_network = NeuralNetwork()
print "随机的初始突触权重："
print neural_network.synaptic_weights
# 训练集。四个样本，每个有3个输入和1个输出
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
# 用训练集训练神经网络
# 重复一万次，每次做微小的调整
neural_network.train(training_set_inputs, training_set_outputs, 10000)
print "训练后的突触权重："
print neural_network.synaptic_weights
# 用新数据测试神经网络
print "考虑新的形势 [1, 0, 0] -> ?: "
print neural_network.think(array([1, 0, 0]))
终极思考 我们用Python打造了一个简单的神经网络。 这样的网络虽然简单好理解，但却是个一根筋，能解决的问题都太简单、有时候幼稚，对于稍微复杂点的局面就应付不了了。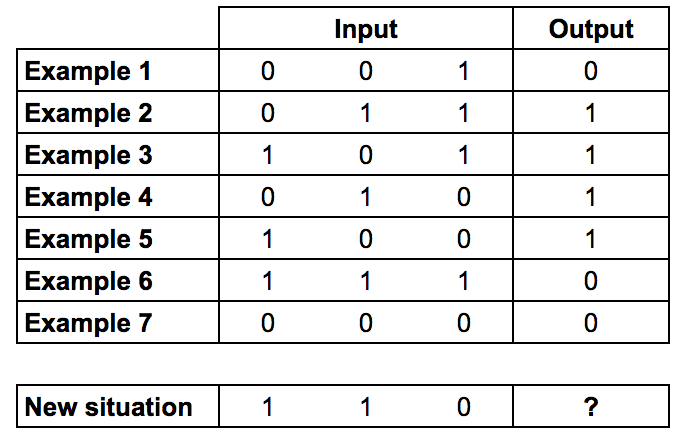 
下表的?处应该是什么？ 经过观察可以发现，第三列是无关的，而前两列成“异或”关系——相等为0，相异为1。所以正确答案应为0。 对于单个神经元来说，这样的线性关系太复杂了，输入-输出之间没有一对一的映射关系。所以我们必须加入一个含4个神经元的隐藏层（Layer 1），这一层使得神经网络能够思考输入的组合问题。 
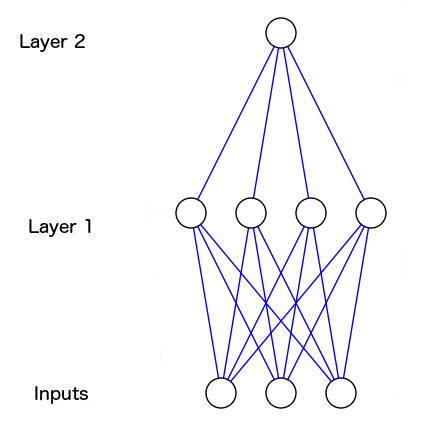由图可见，Layer 1的输出给了Layer 2，如此神经网络就可以学习Layer 1的输出和训练集的输出之间的关系。在学习过程中，这些关系会随着两层的权重调整而加强。 往神经网络中加更多的层，使其思考状态组合，这就是“深度学习”。首先放出代码，之后我会进一步详解。
from numpy import exp, array, random, dot
class NeuronLayer():
def __init__(self, number_of_neurons, number_of_inputs_per_neuron):
self.synaptic_weights = 2 * random.random((number_of_inputs_per_neuron, number_of_neurons)) - 1
class NeuralNetwork():
def __init__(self, layer1, layer2):
self.layer1 = layer1
self.layer2 = layer2
# Sigmoid函数，S形曲线
# 传递输入的加权和，正规化为0-1
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
# Sigmoid函数的导数，Sigmoid曲线的梯度，表示对现有权重的置信程度
def __sigmoid_derivative(self, x):
return x * (1 - x)
# 通过试错训练神经网络，每次微调突触权重
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
for iteration in xrange(number_of_training_iterations):
# 将整个训练集传递给神经网络
output_from_layer_1, output_from_layer_2 = self.think(training_set_inputs)
# 计算第二层的误差
layer2_error = training_set_outputs - output_from_layer_2
layer2_delta = layer2_error * self.__sigmoid_derivative(output_from_layer_2)
# 计算第一层的误差，得到第一层对第二层的影响
layer1_error = layer2_delta.dot(self.layer2.synaptic_weights.T)
layer1_delta = layer1_error * self.__sigmoid_derivative(output_from_layer_1)
# 计算权重调整量
layer1_adjustment = training_set_inputs.T.dot(layer1_delta)
layer2_adjustment = output_from_layer_1.T.dot(layer2_delta)
# 调整权重
self.layer1.synaptic_weights += layer1_adjustment
self.layer2.synaptic_weights += layer2_adjustment
# 神经网络一思考
def think(self, inputs):
output_from_layer1 = self.__sigmoid(dot(inputs, self.layer1.synaptic_weights))
output_from_layer2 = self.__sigmoid(dot(output_from_layer1, self.layer2.synaptic_weights))
return output_from_layer1, output_from_layer2
# 输出权重
def print_weights(self):
print " Layer 1 (4 neurons, each with 3 inputs): "
print self.layer1.synaptic_weights
print " Layer 2 (1 neuron, with 4 inputs):"
print self.layer2.synaptic_weights
if __name__ == "__main__":
# 设定随机数种子
random.seed(1)
# 创建第一层 (4神经元, 每个3输入)
layer1 = NeuronLayer(4, 3)
# 创建第二层 (单神经元，4输入)
layer2 = NeuronLayer(1, 4)
# 组合成神经网络
neural_network = NeuralNetwork(layer1, layer2)
print "Stage 1) 随机初始突触权重： "
neural_network.print_weights()
# 训练集，7个样本，均有3输入1输出
training_set_inputs = array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [0, 1, 0], [1, 0, 0], [1, 1, 1], [0, 0, 0]])
training_set_outputs = array([[0, 1, 1, 1, 1, 0, 0]]).T
# 用训练集训练神经网络
# 迭代60000次，每次微调权重值
neural_network.train(training_set_inputs, training_set_outputs, 60000)
print "Stage 2) 训练后的新权重值： "
neural_network.print_weights()
# 用新数据测试神经网络
print "Stage 3) 思考新形势 [1, 1, 0] -> ?: "
hidden_state, output = neural_network.think(array([1, 1, 0]))
print output
跟上一版代码最大的不同在于，这次有多层。当神经网络计算第二层的误差时，这个误差会被反向传播回第一层，并影响权重值的调整。这就是反向传播算法(Back Propagation)。 虽然看起来很轻松，其实计算机在背后执行了大量的矩阵运算，而且这个过程不是很容易可视化。 原文：How to build a simple neural network in 9 lines of Python code 作者：Milo Spencer-Harper 翻译：Kaiser